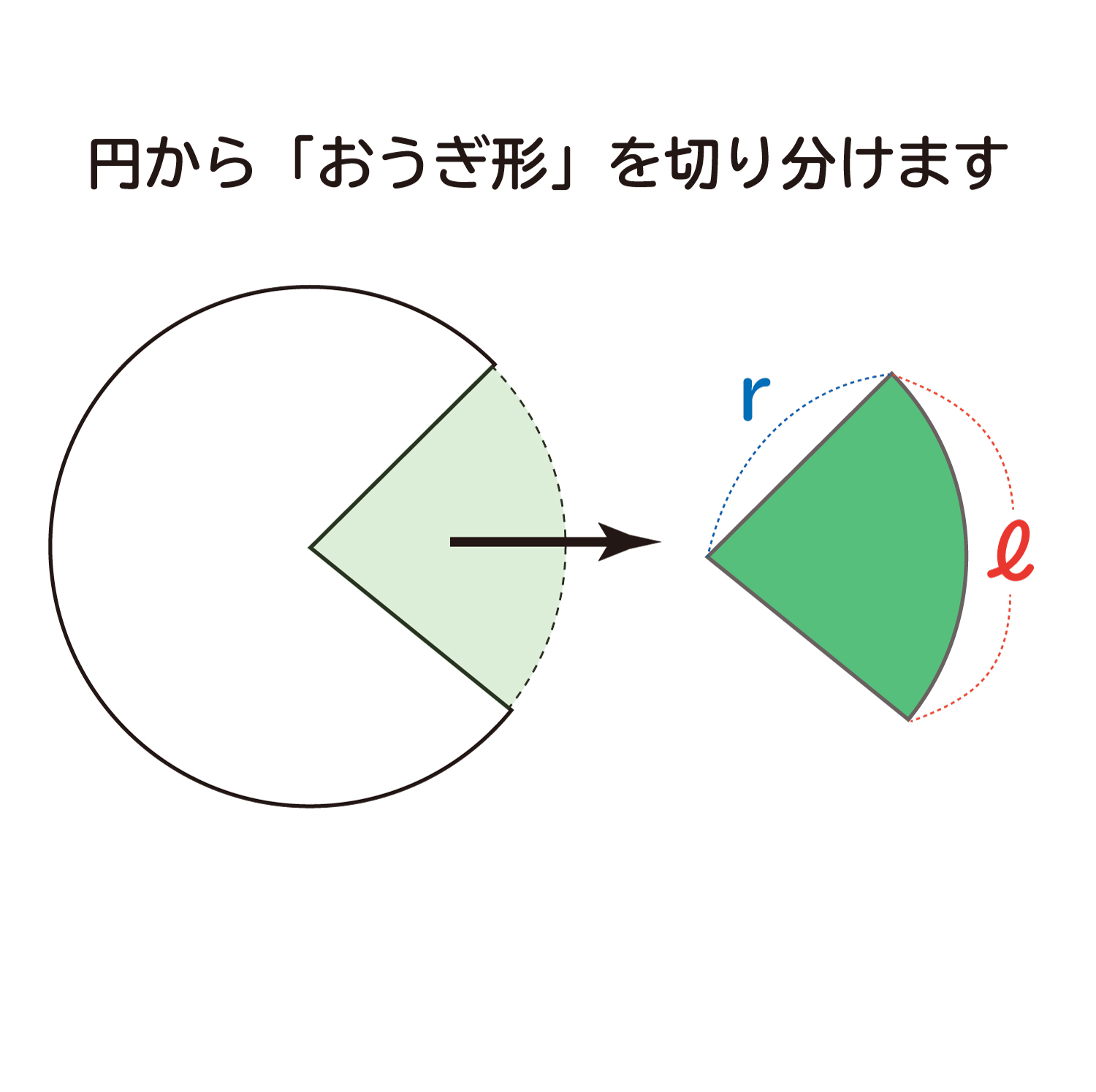
愛されし者 扇形 の 角度 の 求め 方 円錐の表面積の求め方が分かりません それと 扇形の角度のもとめ カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru おうぎ形の弧の長さ ③円の接線の公式 ④2つの円の位置関係 (5)三角関数 ①弧度法 ※θの単位はrad(ラジアン) ②おうぎ形の面積 ※θの単位はrad(ラジアン) おうぎ形の面積=円の面積×おうぎ形の中心角/360度 で求めてみます。 =円の面積×おうぎ形の中心角×1/360 =πr²×180θ/π×1/360 =r²θ×1/2 半径と同じ長さ弧の長さが1ラジアンなので、θラジアンのとき弧の長さxcmとすると 1ラジアン:r cm=θラジアン:x cm x=rθcm 半径r、おうぎ形の弧の長さrθcm おうぎ形の面積=円の面積×おうぎ形の弧の長さ/円周の長さ で求めてみます。

扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ
おうぎ形 面積 公式 ラジアン
おうぎ形 面積 公式 ラジアン-弧度法で弧の長さと面積をだす公式が腑に落ちません 弧の長さは、半径 x 中心角(ラジアン) 面積は、半径 x この長さ x 1/2 とのことですが、なぜ上記の公式で、弧の長さと、面積を求めることができる おうぎ形 面積 弧の長さ 中心角の求め方を問題解説 数スタ 弧度法ってなんだよ ラジアンってなんだよ ってなっている君へ 扇形の弧の長さと面積 数学ii フリー教材開発コミュニティ Ftext



Q Tbn And9gcqfv9ekt Crg9bhcsz7q4t2e8znl6v2tplsqinzmz3lidwdpywk Usqp Cau
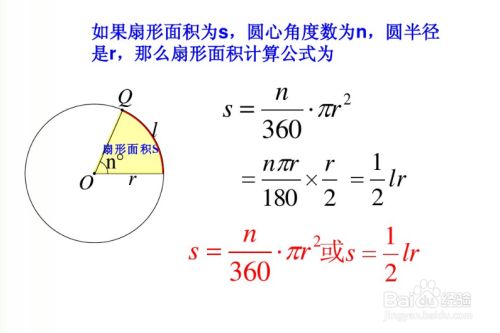
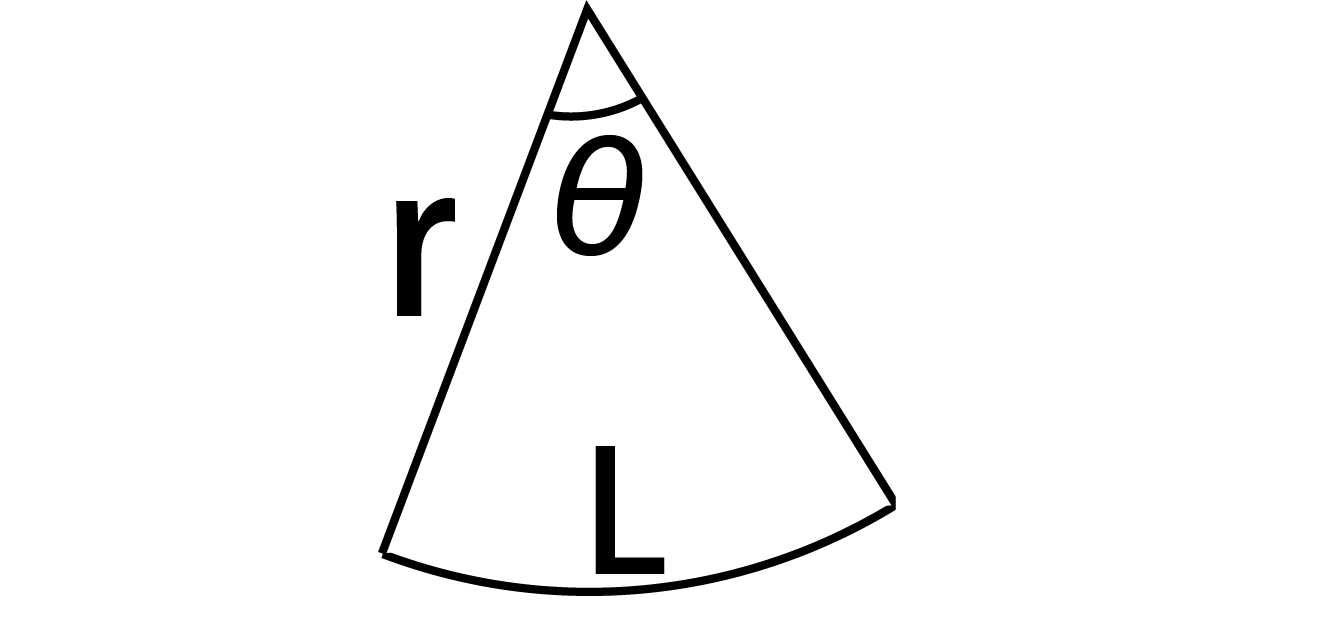
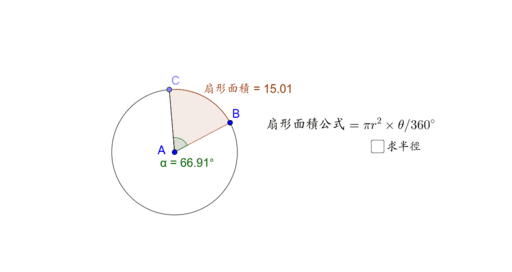
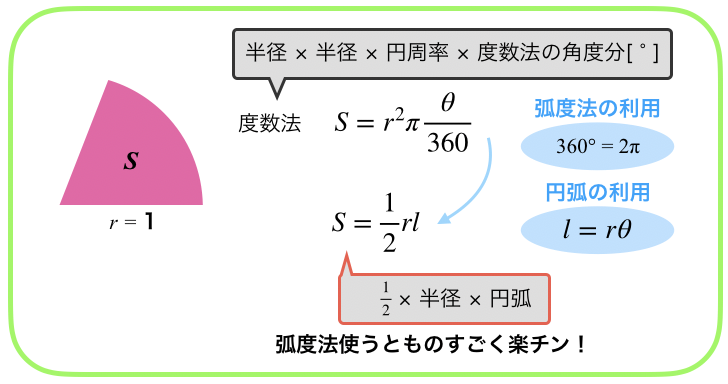
図のように半径が r ,中心角が θ の扇形の弧の長さを l ,面積を S とすると,弧度法の定義より θ = l r だから ∴ l = r θ (1) 面積と中心角の比から S θ = π r 2 2 π ∴ S = 1 2 r 2 θ (2) 以上, (1) , (2) より, S = 1 2 r l となる. 半径8センチ,弧の長さ24センチの おうぎ形の面積を求めなさい。 どのように考えればいいのですか? あと、解説のところに おうぎ形の半径をr,弧の長さをm,面積をsとすると s=1/2mr と書いてあるんですけど、どういう意味ですか? まとめ:扇形の面積は「おうぎ形パワー」を円にかける 扇形の面積の求め方はどうだった? ? 円の公式に毛がはえたようなもんだから、頑張れば覚えられそうだね。 S = πr² × α / 360 「円とおうぎ形」がテストにでるときに確認したいね^^ おうぎ形の
名前に「弧」とついているように,円の弧を使って定義します. 弧度法 半径1の扇形の弧の長さが θ であるとき,この扇形の中心角の大きさを θ rad と定める.ただし, rad は「ラジアン (radian)」と読む. 正確には,「円弧と半径が等しいときの中心角を 1 rad と定める」なのですが,ここでは同値な上の条件を定義としておきましょう. この定義から, 半径1弓形の公式 面積 弧の長さ 弦の長さ 数学 エクセルマニア 中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット 円周怪獣ラジアン 14 1改訂版 ラジアン Rad は量の単位としてはやや特殊なものです これは 同じ三角形の面積(3辺からヘロンの公式) 三角形の面積(1辺と2角から) 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから)
おうぎ形の面積は弧の長さ×半径して/2説明しよう。#中学数学 #中1数学 #平面図形 #おうぎ形 #テスト対策 #家庭学習 公式チェック 度数法を弧度法に直すには? 度数法を 180で割って 「°」を取り 「 p i p i 」をつける。 言えなかった人はもう一度閉じて、言ってみて下さい。 覚えたと思ったら、例題に進 おうぎ形の面積を求める公式 面積=円の面積×中心角の割合 半径5cm、中心角36度のおうぎ形の面積は何cm 2 計算方法は加減法または代入法で選択でき、途中式も表示されます。



おう ぎ 形 の 面積 求め 方




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット
② 求積公式を基にして,三角形や平行四辺形などの面積を求めること (2)本単元の目標 関心・意欲・態度 数学的な考え方 技能 知識・理解 既習の面積公式を基に, 三角形や平行四辺形などの 面積を求める公式を進んで 見いだそうとしている。 三角形の面積の公式に似ています。 おうぎ形を、中心角が上になるように配置してみましょう。 底辺が曲線になってはいるけれど、おうぎ形は三角形にちょっと似ていますよね。 三角形で底辺にあたりものは、おうぎ形では、弧。見た目が変になりますが、合っているので心配なく! おうぎ形の弧の長さ、面積の公式 演習問題で理解を深める! おうぎ形の中心角の求め方 演習問題で理解を深めよう! 円とおうぎ形の公式 まとめ;




高校数学 一般角と弧度法 扇形の弧長l R8と面積s 1 2r 8 受験の月




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
《円・半円・弧・扇形》の円周・面積の求め方と公式一覧 2)扇型の面積と重心 明治大学;扇形の面積は、r 2 θ/2で計算できます。 rは半径、θは角度(ラジアン)です。 なお、円の面積はπr^2ですね。 扇形の面積の公式に、θ=2πを代入すると円の公式と同じになります。 今回は扇形の面積の意味、公式と求め方、ラジアンとの関係について説明します。 ラジアン(弧度)の意味が曖昧な方は下記も参考になります。 弧度法とは? 1分でわかる意味と角度からラジアンの変換は下記が参考になります。 扇形的弧長與面積公式: 若圓半徑為 r ,扇形 COD 的圓心角 ∠ COD =θ(弧度),0 ≤ θ ≤ 2π, 如下圖所示,令扇形的弧長為 s ,面積為 A ,則: おうぎ形




おうぎ形の面積と弧の長さの公式 全国 中学数学ができるようになるブログ




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか
扇形の面積 S=r^2θ/2=rL/2 上式の通り、扇形の面積は、扇形の弧の長さLに半径rを掛けて2で除した値です。扇形の面積は下記が参考になります。 扇形の面積は?1分でわかる意味、公式、求め方、ラジアンとの関係 扇形の弧の長さとラジアンの関係 もしおうぎ形ではなく円であれば、面積は πr2 π r 2 なので、比で考えると S πr2 = θ 2π S π r 2 = θ 2 π なので、これを S S について解くと S = 1 2r2θ S = 1 2 r 2 θ となります。 もちろんこれでもいいのですが、弧の長さの式を使ってさらに変形することもできます。 弧の長さを l l とすると、 l = rθ l = r θ なので、 S = 1 2rl S = 1 2 r l となります。 この式変形は単純ですR = h/2 c^2/8h となります。 アンケートにご協力頂き有り難うございました。 送信を完了しました。 弓形の面積(弓形の弦長と高さから) のアンケート記入欄 性別 男 女 年齢 歳未満 歳代 30歳代 40歳代 50歳代 60歳以上



扇形 面積 公式 扇型の面積と中心角の求め方 扇型の問題は円の公式の理解がカギ Documents Openideo Com




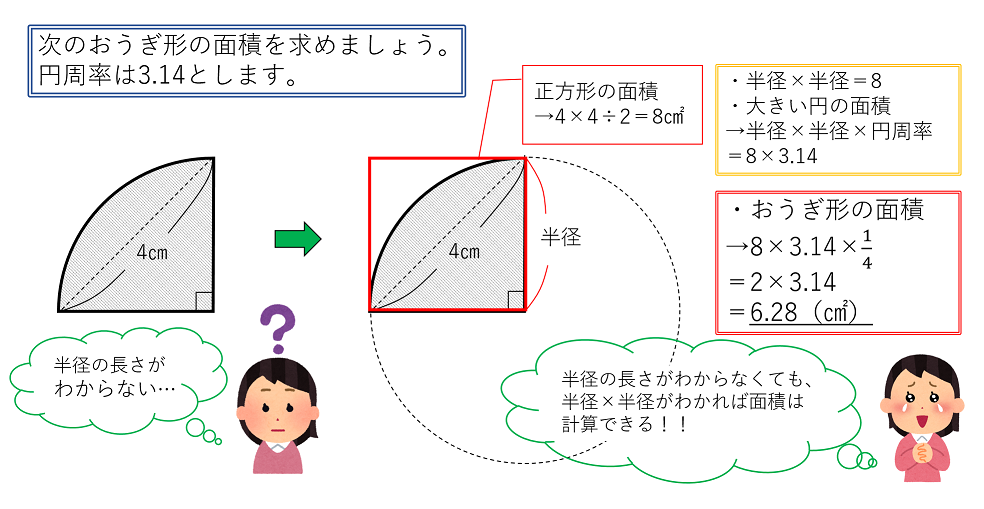
標準 おうぎ形と正方形の面積 なかけんの数学ノート
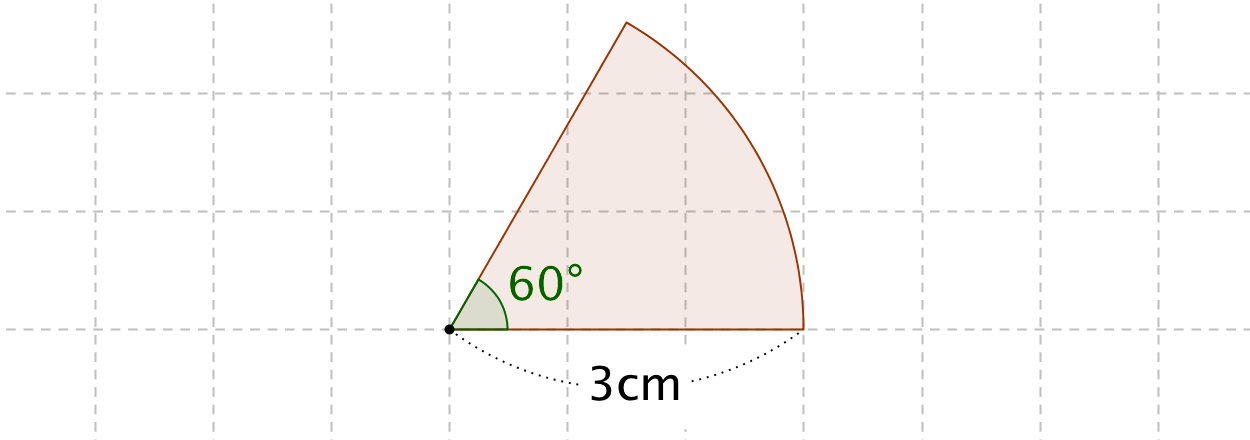
扇形の面積の公式と求め方 扇形の面積の公式は下記です。 S=r 2 θ/2 ※Sは扇形の面積、rは扇形の半径、θは扇形の角度(単位はラジアン) 公式を用いて、例題の扇形の面積を求めましょう。角度60 の扇形があります。半径が6です 扇の面積おうぎ形の弧の長さ、面積、中心角の求め方と公式 Irohabook 扇形の弧の長さの求め方 公式と計算例 中学数学3分で簡単にわかる!「扇形(おうぎ形)の面積の ★扇形の中心角の求め方★途中式をていねいに解説!面積、弧半径が等しいおうぎ形の面積は,中心角の大きさに比例する。 したがって, おうぎ形の面積 : 円の面積 = おうぎ形の中心角 : ラジアン(360°)




弧




扇形 面積 公式 扇型の面積と中心角の求め方 扇型の問題は円の公式の理解がカギ Documents Openideo Com
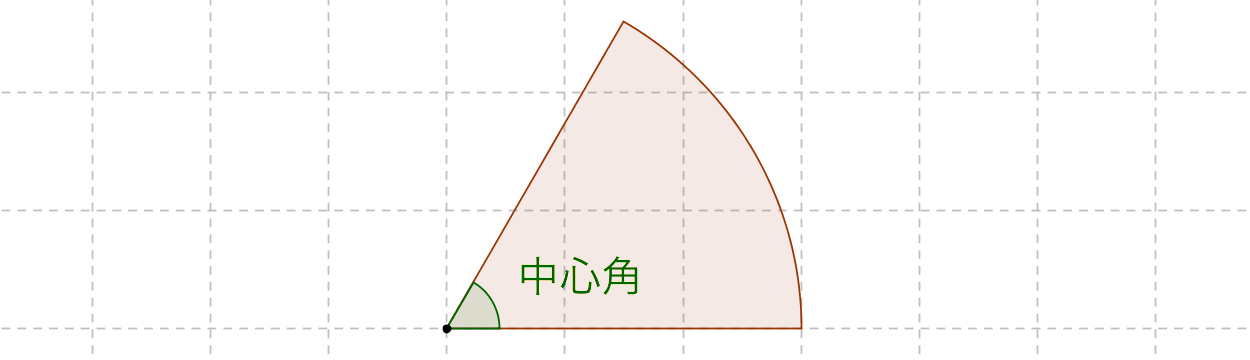
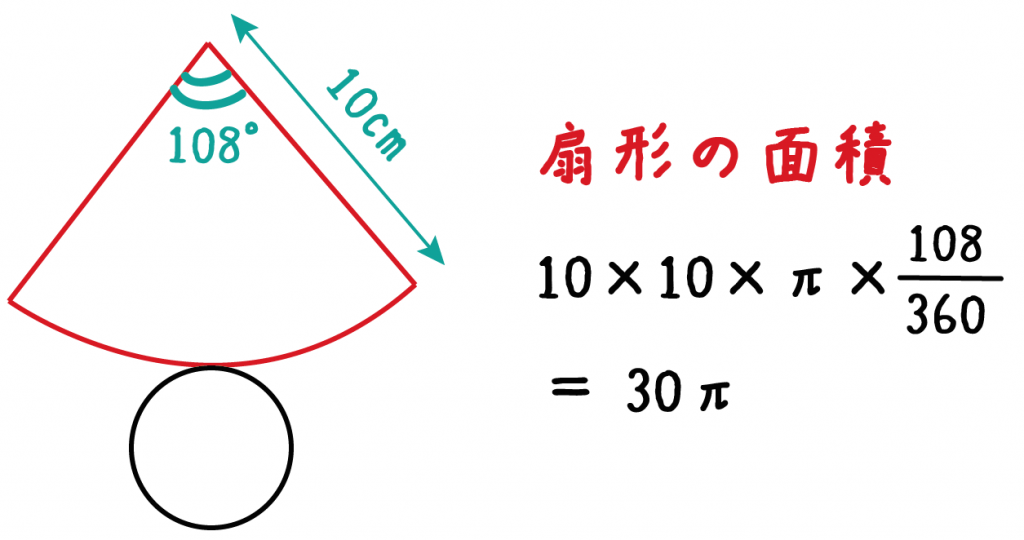
②おうぎ形の面積 今度は,面積 $S$ を求めてみましょう。 おうぎ形の面積は,円の面積に $\cfrac{\text{中心角}}{1周分の角} $ をかけて求められます。半径 5cm, 面積 πcm 2 のおうぎ形 点Oを極とする極座標表示で表された曲線上の点をPとするとき,線分OPの通過領域の面積を求める際に,強力な威力を発揮するのが扇型分割による積分です,ここではこの積分公式の証明を行います. 1.扇形分割の積分公式A = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) A = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) 弓形 こんにちは おうぎ形の面積の公式と弧の長さの公式は、次の式で表されますね^^ 前半のπr^2(πr2乗)は、円の面積=半径×半径×円周率2πrは、円周=直 円




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ



Www Nhk Or Jp Kokokoza Library Radio R2 Math2 Archive 16 Suu2 50 Pdf
おうぎ形の面積の求め方2 もう一つのおうぎ形の面積の求め方は円の面積を求めてから、そこから中心角を用いておうぎ形を求める方法です。 まずは簡単におうぎ形の中心角が $60^{\circ}$ の場合を考えます。 ラジアンがないと困る,というよりも,ラジアンがないと不便だという場面は結構あります。 と言っても,高校数学でいえば数学Ⅲ以降の話になりますし,数学全体では「解析学」(微分積分)の分野です。 生徒の皆さんが最初に習うのは 「扇形公式半径と中心角から面積を求める式から、上の式を導いてみましょう。 S = πr2 × x 360 = π× r×r× x 360 = (2πr× x 360)× 1 2 × r S = π r 2 × x 360 = π × r × r × x 360 = ( 2 π r × x 360) × 1 2 × r ここで、弧の長さ l は l = 2πr× x 360 l = 2 π r × x 360 であるから S = l× 1 2 ×r = 1 2lr S = l × 1 2 × r = 1 2 l r となるのです。 続いては、扇形の面積を求める計算問題を解いてみましょう!




扇 おうぎ 形の面積を求める公式と弧の長さの求め方




おうぎ形の問題 パターンを知ろう 苦手な数学を簡単に




中1 中1 数学 範囲 おうぎ形の中心角の求め方 大放出ぅ 中学生 Clear




おうぎ形 色のついた面積の求め方 数学の記録




半径6cm 弧の長さ2pcmのおうぎがたの面積 はどーやって求めますか Clear



1




この問題の式の2pって 直径を求めるの12 2の2 半径 2 Clear



Q Tbn And9gcqfv9ekt Crg9bhcsz7q4t2e8znl6v2tplsqinzmz3lidwdpywk Usqp Cau




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学



扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ




扇形面積公式弧長 3分で分かる 扇形 おうぎ形 の面積と弧の長さの Mtlpe



おうぎ形の面積の公式 算数の公式




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



3




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




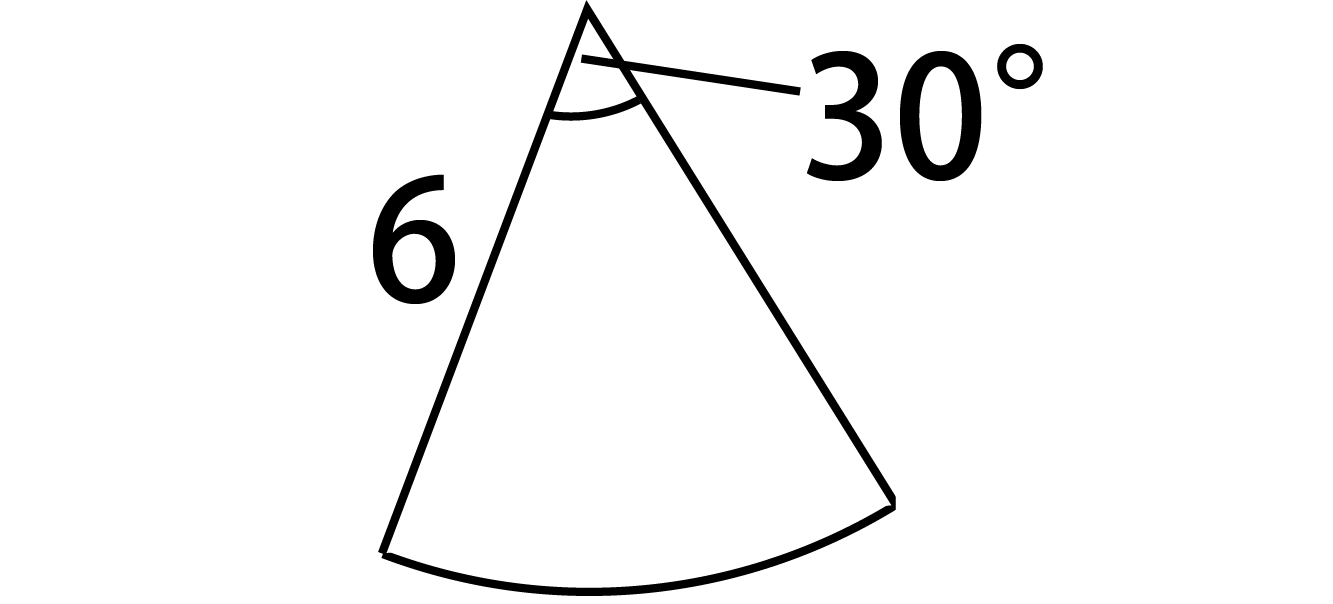
数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



おうぎ形の面積の公式 算数の公式



扇形 面積 公式 扇型の面積と中心角の求め方 扇型の問題は円の公式の理解がカギ Documents Openideo Com




印刷可能 おうぎ形 面積 公式 ニスヌーピー 壁紙
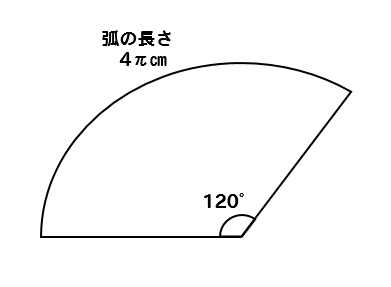



おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ




おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ



おう ぎ 形 の 面積 求め 方



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典




扇形の面積の求め方 公式と計算例
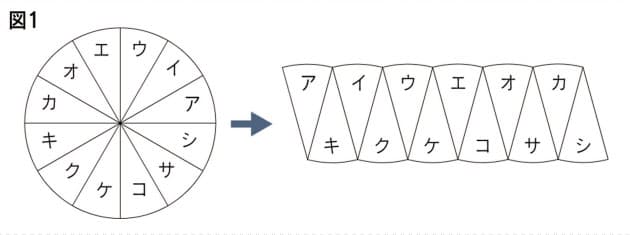



子供に説明できる 円の面積の公式 の証明 Nikkei Style




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ



扇形の半径と面積が分かっているときの中心角の求め方を教えてください 例 Yahoo 知恵袋




扇形面積公式弧長 3分で分かる 扇形 おうぎ形 の面積と弧の長さの Mtlpe




簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ
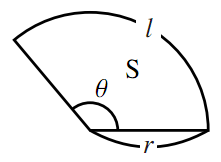



扇形の弧の長さと面積 数学ii フリー教材開発コミュニティ Ftext




質問です ゞ この公式の証明方法が何を表したいのかが全く分かりません Clear




三角関数公式 大学受験の王道




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
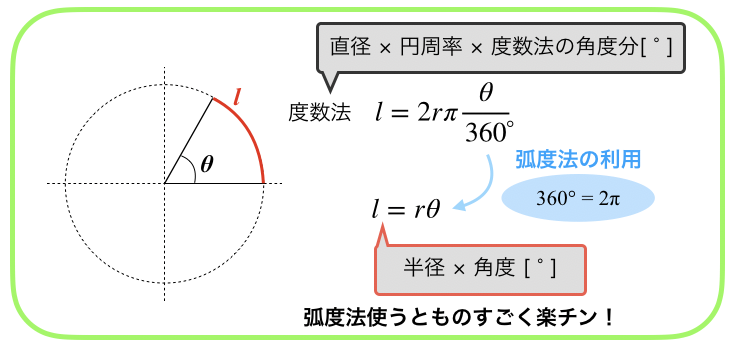



弧度法ってなんだよ ラジアンってなんだよ ってなっている君へ 動画解説あり
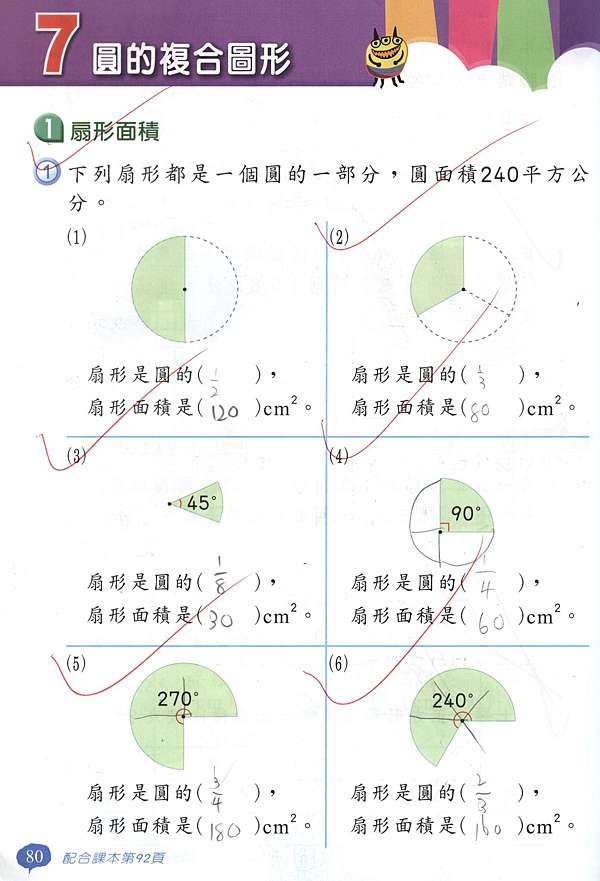



扇形 面積 公式 扇型の面積と中心角の求め方 扇型の問題は円の公式の理解がカギ Documents Openideo Com




おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ




2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく




扇形の弧の長さ 扇形の面積 弧度法 一夜漬け高校数学274 三角関数 Youtube
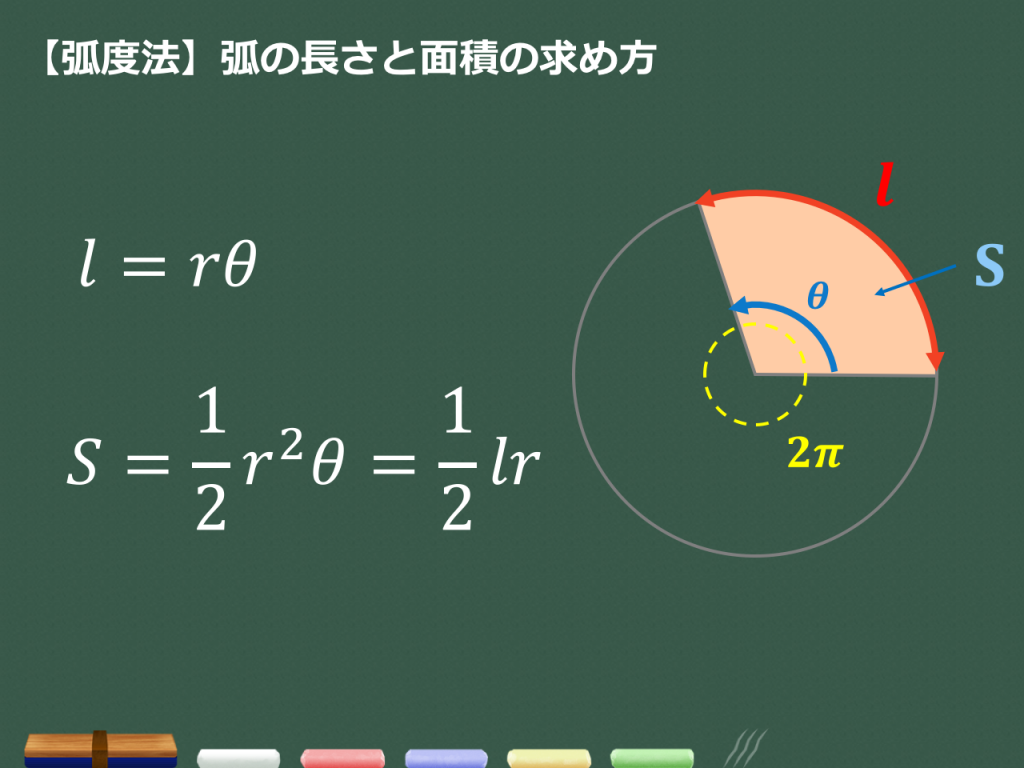



3分でわかる 弧度法 ラジアン の要点 度数法との変換 合格サプリ



三角形と扇形の面積 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典




おうぎ形の面積と弧の長さ Geogebra



ダウンロード 扇形 中心 角 求め 方 ニスヌーピー 壁紙



1




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題




扇形面積の求め方 扇形の面積公式が一目でわかる 丁寧な証明付き 高校 Qkaxtw




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット



扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ



弧




裏技 おうぎ形の面積を一瞬で求める 弧の長さを利用した裏技公式 中学数学 平面図形 2 Youtube




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典



扇形 弧の長さ 公式 ニスヌーピー 壁紙




おうぎ形の面積 弧度法との関連から眺める 身勝手な主張




おうぎ形の中心角の求め方を教えて下さい Clear




数学質問 おうぎ形の面積の公式について Youtube




数ii 三角関数弧度法 弧の長さ 扇形の面積 Youtube




おうぎ形の面積 弧度法との関連から眺める 身勝手な主張



おう ぎ 形 の 面積 求め 方




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題




扇形の面積の求め方 公式と計算例
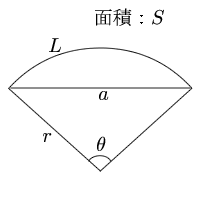



扇形 面積の計算 計算サイト




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ




標準 おうぎ形と正方形の面積 なかけんの数学ノート
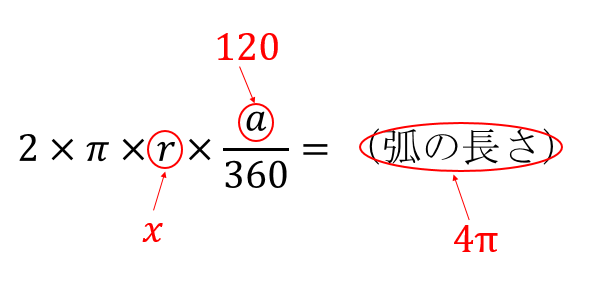



おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ



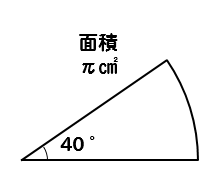
半径9cm 面積18pcm の扇形の中心角を求めなさいという問 Yahoo 知恵袋




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題



半径4cm 中心角225 のおうぎ形の弧の長さと面積の求め方と答 Yahoo 知恵袋



弧度法ってなんだよ ラジアンってなんだよ ってなっている君へ 動画解説あり



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典




標準 おうぎ形と正方形の面積 なかけんの数学ノート




円弧面積の計算式




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



おう ぎ 形 の 面積 求め 方



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典



おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




円錐の側面積 展開図の扇形の中心角 扇形の面積の求め方について 身勝手な主張




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ




おうぎ形の問題 ちょっと応用編 切り取って求める 苦手な数学を簡単に




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




扇形面積公式弧長 3分で分かる 扇形 おうぎ形 の面積と弧の長さの Mtlpe


